Что такое капитализация процентов?
Большинство из нас привыкли определять выгодность любых вложений по размеру годовой процентной ставки. Но это не единственный показатель, на который стоит ориентироваться при выборе инструмента. Большое значение имеет метод начисления процентов.
Первый, и наиболее распространённый, вариант — простой процент, когда начисление прибыли осуществляется однократно по окончании действия договора на первоначальную сумму вложений. Вторая схема, менее привычная, но более выгодная — сложный процент, когда выплаты по процентам возрастают по экспоненциальному графику. Давайте подробнее разберём, что это значит.
Суть метода в том, что каждый период (ежемесячно, ежеквартально или ежегодно) сумма инвестиций увеличивается на определённый процент, и в следующем периоде проценты начисляются уже на большую сумму, тем самым увеличивая итоговую прибыль. В народе этот эффект называют незамысловатым «проценты на проценты», в финансовой среде — сложным процентом, реинвестированием или капитализацией процентов.
Инвестиции с капитализацией процентов подходят тем, кто ищет варианты долгосрочных вложений, минимум на год, а ещё лучше — на пять или десять. Хоть процентная ставка и остаётся неизменной, прибыль будет постепенно расти, поскольку размер вложений с определённой периодичностью пополняется накопленным доходом.
Чтобы лучше понять, как работает этот процесс, рассмотрим, как происходит начисление простых и сложных процентов на одну и ту же сумму вложений.
Инвестиции без капитализации процентов
Предположим, что на вашем брокерском счёте есть 100 000 рублей. Вы решили инвестировать их в ценные бумаги на 10 лет под 30% годовых. При этом прибыль в виде дивидендов или купонов по облигациям вы будете тратить на личные нужды. То есть сумма вложений останется неизменной на протяжении всего срока.
Как будет происходить прирост прибыли:
Для вашего удобства мы создали инвестиционный калькулятор сложного процента с пополнением, сделать рассчеты в котором можно онлайн.
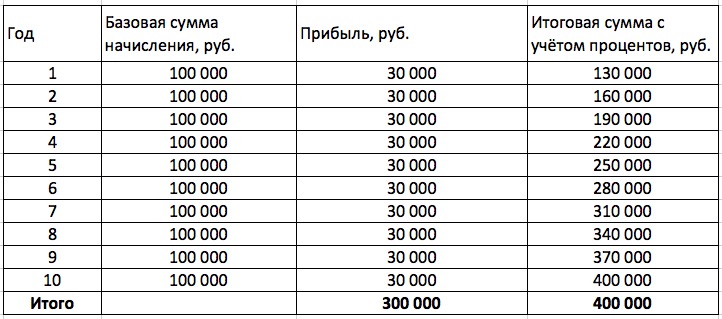
Впечатляет, но только до тех пор, пока мы не рассмотрели второй вариант.
Инвестиции с капитализацией процентов
Теперь представим, что на вашем втором счёте, ИИС, есть ещё 100 тысяч рублей, которые вы так же планируете инвестировать под 30 % годовых на 10-летний срок. Но при этом не станете тратить прибыль, которая раз в год будет поступать к вам в виде дивидендов или купонного дохода, а повторно инвестируете её под тот же процент.
Прирост будет происходить следующим образом:
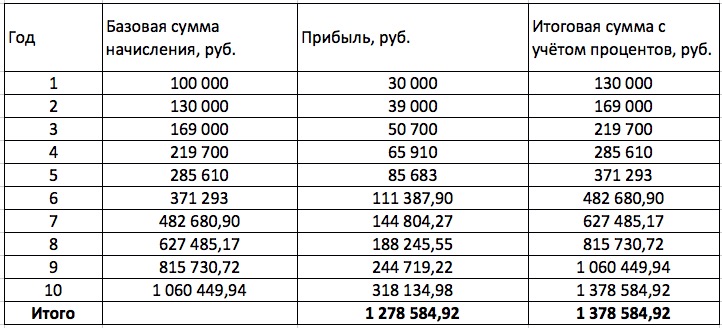
Разница между суммой, рассчитанной с помощью простого процента, и размером начислений при реинвестировании составляет почти миллион рублей. Согласитесь, это более чем серьёзные деньги.
Чтобы самостоятельно рассчитать итоговую сумму по сложным процентам, используйте формулу:
X = S * (1 + П / 100) N , где:
X — размер вашего капитала в конце срока;
S – сумма на начало накоплений;
П — процент, начисляемый за период, за который производится капитализация (месяц, квартал, год);
N — количество периодов капитализации в общем сроке вложения капитала.
Обратите внимание, что в большинстве инвестиционных программ указан годовой процент (вне зависимости от срока вложений). К примеру, если вы инвестируете на 9 месяцев под 12% годовых с капитализацией процентов один раз в квартал, то П в этом случае будет равен 0,03% (12% / 4 / 100), а N — 3.
Отличный пример заработка на сложных процентах — история Бенджамина Франклина. В 1791 году он положил на банковский депозит $5000 и завещал их городским управлениям Филадельфии и Бостона. Но с одним условием: снять эти деньги можно было только через 100 и 200 лет. В 1891 году, по прошествии первого столетия, было снято 500 тысяч долларов, впоследствии потраченные на общественные работы. А ещё через сто лет, в 1991-м, на счёте оказалось уже 2 миллиона долларов.
Магия сложного процента в инвестициях
Понятно, что приведённые выше 30% годовых, это абстрактная цифра, и в реальности доход по ценным бумагам, особенно низкорисковым, может быть ниже.
Чтобы понять, сколько можно заработать на акциях и облигациях с помощью сложных процентов, обладая даже небольшой суммой, произведём нехитрый расчёт. Предположим, у вас есть 100 тысяч рублей и 20 лет до достижения какой-либо финансовой цели (например, пенсии). Разделим эти деньги пополам и инвестируем их в облигации под 10% годовых на 20 лет. Только в первом случае вся полученная прибыль будет сниматься с брокерского счёта и тратиться, а во втором — инвестироваться в ИИС вместе с основной суммой под тот же процент. Разница очевидна:
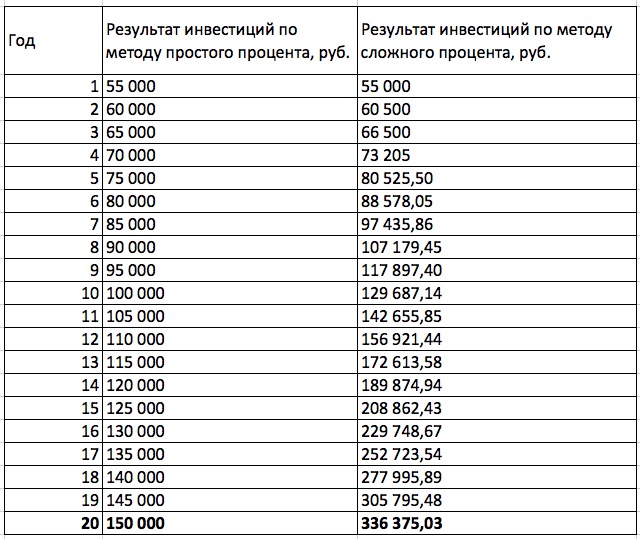
Вот что значит капитализация, или магия сложного процента: срок тот же, процент тоже, а прибыль выше в 2,2 раза. Секрет прост: чтобы сложный процент раскрыл свой потенциал и наращивал действительно хорошую прибыль, нужно инвестировать на довольно продолжительный срок.
И в заключение хотим добавить, что Альберт Эйнштейн называл сложные проценты «самой могущественной силой во Вселенной», барон Ротшильд, самый богатый человек своего времени, — «восьмым чудом света», а великий Уоррен Баффетт заработал с их помощью львиную долю своего состояния.
Вам будет ещё удобнее — специалисты компании «Открытие Брокер» помогут подобрать подходящую стратегию и проконсультируют по всем вопросам.
Наращенная сумма
Под наращенной суммой долга (ссуды, депозита и т.д.) понимают первоначальную сумму с начисленными процентами к концу срока. Наращенная сумма определяется умножением первоначальной суммы на множитель наращения, который показывает, во сколько раз наращенная сумма больше первоначальной:
где У — наращенная сумма, руб.;
Р — первоначальная сумма, руб.; q — множитель наращения.
Множитель наращения при начислении простых и сложных процентов будет различен.
Множитель наращения при начислении простых процентов рассчитывается по формуле
а наращенная сумма — по формуле
где п — срок наращения, период;
Если ставка процентов годовая, а проценты уплачиваются в течение года, то необходимо определить, какая часть годовых процентов уплачивается кредитору за период. Для этого срок наращения рассчитывают по формуле

где ? — число дней, по истечении которых начисляются и выплачиваются проценты;
К — количество дней в году.
Пример. Кредит в размере 1 млн руб. выдан 20 января до 5 октября включительно (на 258 дней) под 18% годовых. Проценты простые. В этом случае наращенная сумма составит

В кредитных соглашениях иногда предусматриваются изменяющиеся во времени процентные ставки — «плавающие» ставки. Если это простые ставки, то наращенная на конец срока сумма определяется из выражения


Пример. Кредитный договор предусматривает следующий порядок начисления процентов: первый год — ставка 16%, в каждом последующем полугодии ставка повышается на 1%. Необходимо определить множитель наращения за 2,5 года:
В практических задачах иногда возникает необходимость в решении вторичных задач — определении срока наращения или размера процентной ставки в том или ином ее виде при всех прочих заданных условиях.
Продолжительность срока наращения в годах или днях может быть определена из решения уравнения:
Из этого уравнения получаем

Срок в днях будет рассчитан по формуле

Пример. Определим продолжительность займа в днях, для того чтобы долг, равный 1 млн руб., вырос до 1,2 млн руб., при условии, что начисляются простые проценты по ставке 25% годовых (К = 365 дней).

Аналогично может быть определена величина процентной ставки. Такая необходимость в расчете процентной ставки возникает при определении доходности заемной операции и при сравнении контрактов по их доходности в случаях, когда процентные ставки в явном виде не указаны. Аналогично первому случаю получаем

Пример. В договоре займа предусматривается погашение обязательства в сумме 110 млн руб. через 120 дней. Первоначальная сумма долга — 90 млн руб. Необходимо определить доходность заемной операции для заимодавца в виде годовой ставки процента. Получаем

Множитель наращения при начислении сложных процентов рассчитывается по формуле
Я = 0 + 0«,

а наращенная сумма — по формуле Проценты (У) будут равны:

В случае использования «плавающих» ставок сложных процентов наращенная сумма рассчитывается по формуле

где — значение ставки за период щ.
Поскольку множитель наращения при простых и сложных ставках различен, то наблюдается следующая закономерность. Если срок наращения меньше года, то
Стоимость денег, типы процентов, дисконтирование и форвардные ставки. Ликбез для гика, ч.1
Представьте себе ситуацию – вы покупаете машину, и вам предлагают два варианта: заплатить с рассрочкой в несколько месяцев или погасить всю сумму сразу и с небольшой скидкой. Какой окажется выгоднее?
Или, например, вы хотите разместить вклад на год. Можно положить на весь срок под высокий процент или на отдельные короткие сроки под более низкий. Что лучше и насколько?
Все ответы под катом. И добро пожаловать в мир, где время — всегда деньги. До этого вы знали об этом, но теперь — в деталях и с примерами.
Меня зовут Мария Абрашкина, я математик и Product Owner в команде по расчету портфельных рисков. А также один из авторов видеокурса про финансовую математику (Ч.1 – Типы начисления процентов, Ч.2 – Дисконтирование, Ч.3 – Форвардные процентные ставки). В этом посте я расскажу о стоимости денег, процентных ставках и облигациях. Эти знания помогут вам в будущем принимать финансовые решения основываясь на точном расчете, используя простую математику.

#1. Временная стоимость денег. Типы начисления процентов
Сначала поговорим о том, что такое временная стоимость денег, или Time Value of Money (TVM), почему деньги имеют стоимость и какие виды процентов существуют.
На картинке ниже показан список фильмов с максимальными кассовыми сборами.

Можем ли мы их сравнить по этим цифрам? Учитывая, что фильмы выходили в разные годы, вряд ли такое сравнение будет правильным. Как быть?
Давайте рассмотрим более простой пример. Допустим, у вас есть тысяча рублей, и я у вас прошу эту сумму в долг. Сколько вы хотите, чтобы я вам отдала через год? Возможно, вы подумаете, что на эту тысячу рублей вы сейчас можете купить бутылку вкусного вина или что-то другое. Также вы можете предположить, что через год на ту же самую тысячу рублей вы вряд ли сможете купить этот товар по причине инфляции. Кроме того, существует риск, что деньги я не верну. Поэтому, скорее всего, вы захотите компенсацию за то, что вы пока не будете покупать бутылку вина или какую-нибудь другую вещь. Также вам необходим стимул, оправдывающий риск того, что деньги я вам могу и не вернуть. Вероятно, вы потребуете от меня вернуть деньги с какой-то надбавкой, то есть с процентом.
Итак, деньги имеют стоимость, потому что их владелец хочет компенсации за то, что он не может купить какой-то товар или услугу, и за риск, который он несет, давая деньги в долг.
На языке математики это будет выглядеть так:
Сейчас вы мне даете тысячу рублей. Обозначим это как PV (Present Value) . Допустим ставка (r) равна 5%, и деньги вы даете мне сроком на один год. Тогда возвращая деньги FV (Future Value) , мне придется добавить к исходной сумме 50 рублей.
Если записать эту формулу в общем виде, то будущее значение равняется сумме долга, умноженной на единицу плюс процентная ставка.

А что, если начисление процентов происходит не раз в год, а чаще? Или что если проценты начисляются в течение двух, трех, десяти лет? В данном случае нам нужно всегда уточнять, каким образом происходит начисление процентов, в конце срока или с какой-то периодичностью и на сколько лет.
Простые проценты
Рассмотрим пример, когда проценты начисляются в конце срока вклада. Будущее значение будет равняться текущему значению плюс текущее значение, умноженное на годовую процентную ставку. Годовая процентная ставка будет прибавляться к сумме нашего вклада столько раз, на сколько лет мы сделали вклад.

Результат – текущее значение, умноженное на сумму единица плюс процентная ставка (r) , умноженная на число лет вклада (T) . Такой способ начисления процентов называется простыми процентами.
Рассмотрим ситуацию с начислением за период в несколько лет. Считаем, что действующая процентная ставка на протяжении всего периода будет одинаковая. Тогда формула принимает следующий вид: текущее значение, умноженное на сумму единица плюс процентная ставка, затем еще раз на сумму единицы и процентной ставки и т. д. Умножать следует столько раз, на какое количество лет был сделан вклад. В общем виде формула будет выглядеть следующим образом:
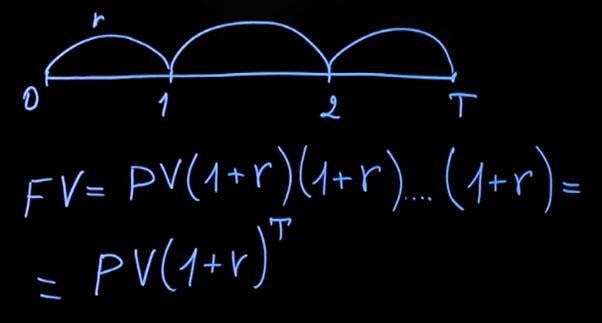
Обратите внимание – если в первом случае к нашему вкладу каждый год прибавлялась сумма процентов (как в первом примере, где добавлялось к сумме вклада 50 рублей), то в случае с ежегодным начислением на 50 рублей, добавленные в первом периоде, у нас каждый раз начисляется процент.
Всегда важно обращать внимание на то, каким образом происходит начисление процентов. Проценты могут начисляться не только раз в год, но и раз в полгода, каждый день. И в принципе нам ничего не мешает начислять эти проценты непрерывно.
Непрерывное начисление процентов
Давайте рассмотрим, как будет выглядеть формула для начислений процентов чаще одного раза в год. В этом случае будущее значение будет равняться текущему значению, умноженному на сумму единица плюс годовая процентная ставка, деленная на количество периодов начислений в году (n) в степени nT . Если начисления производятся каждые полгода, то n=2 , если каждый день, то n=365 .

Как же будет выглядеть формула, если мы хотим начислять проценты непрерывно? Тут придется вспомнить школьную математику. Формула будет следующей:
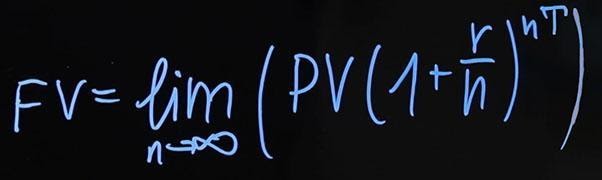
Для того, чтобы привести наш предел к какому-то удобному виду, нам нужно сделать подстановку. В итоге мы получаем следующее:
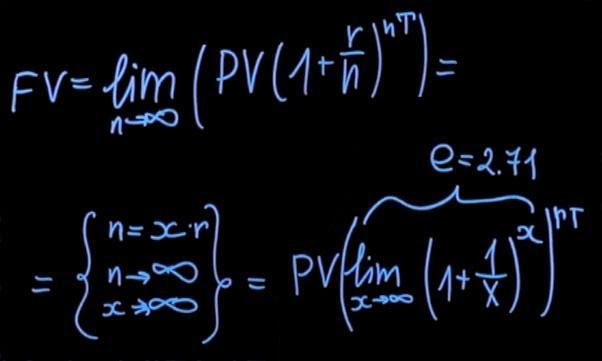
С учетом того, что наш предел равен числу Эйлера (е=2,71), наша формула преобразуется в очень простое выражение. Текущее значение нашего вклада умножается на экспоненту, которая возводится в степень, представленную произведением процентной ставки и количества лет, на которые начисляются наши проценты.

Давайте сравним, как выглядят платежи в зависимости от периодичности начислений. В таблице представлено будущее значение вклада в сто тысяч рублей, который положен на десять лет по ставке двадцать процентов.
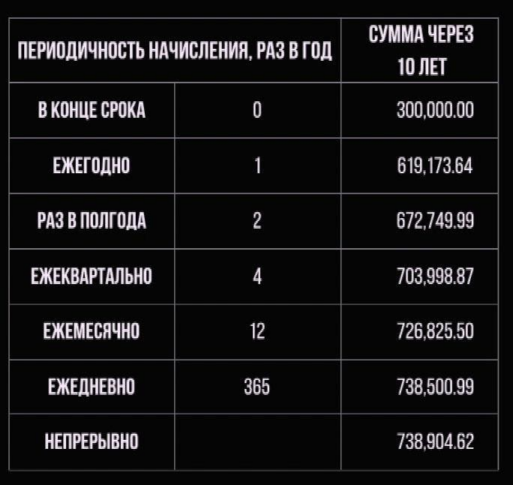
Как вы можете видеть – 300 тысяч рублей вкладчик получит в случае, если начисления производятся в конце срока действия вклада.
Таким образом сумма вклада при начислении процентов ежегодно в два раза превышает сумму вклада при выплате процентов единожды в конце срока.
Если же начисления производятся непрерывно, то сумма вклада оказывается более 700 тысяч рублей против 300 тысяч рублей при простом начислении процентов.
На графике ниже наглядно показано, как растет итоговая сумма вкладов при разных способах начисления процентов.
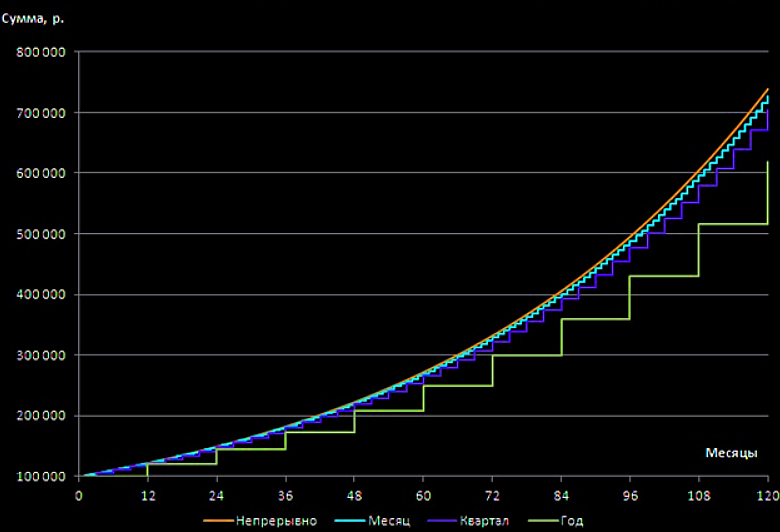
Отсюда необходимо сделать вывод:
выбирая вклад, важно смотреть не только на размер процентной ставки, но и на периодичность начисления процентов. Высокая процентная ставка не всегда является по-настоящему выгодной.
Поэтому, перед тем как сделать свой выбор, имеет смысл сделать небольшие вычисления, чтобы узнать итоговую сумму вклада при заданных условиях.
#2. Дисконтирование (помогает понять, что лучше: взять рассрочку или заплатить сейчас со скидкой)
Мы рассмотрели, какие бывают ставки и какие бывают способы начисления процентов. Если проценты выплачиваются в конце срока действия вклада, проценты называются простыми, если проценты выплачиваются с какой-то периодичностью, то такие проценты называются сложными.
Давайте решим обратную задачу. Допустим, мы знаем, сколько нам заплатят в будущем (например, нам кто-то пообещал платеж за какой-то продукт). Мы также знаем, какая сейчас процентная ставка. Как нам посчитать текущую цену этого продукта?
Как было сказано ранее, будущее значение суммы платежа будет равняться текущему значению, умноженному на единицу плюс процентная ставка. Если из этой формулы мы выразим текущее значение, то оно будет равняться будущему значению, деленному на единицу плюс процентная ставка.

Если проценты начисляются с какой-то периодичностью, то в общем виде формула выглядит так:
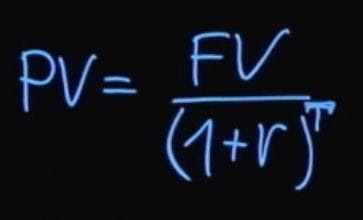
T – это количество периодов выплат начислений процентной ставки. Такой процесс деления будущего значения на единицу плюс процентная ставка в степени T называется дисконтированием. А множитель, единица деленная на сумму единицы плюс r в степени T , называется коэффициентом дисконтирования.
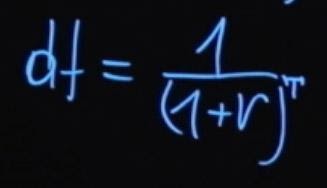
Давайте вернемся к задаче о том, какую премию лучше выбрать. В зависимости от способа премирования сумма выплат может отличаться. При этом не всегда очевидно, какой из способов предпочтительнее. Чтобы дать правильный ответ, необходимо решить математическую задачу. Предположим, у нас есть возможность взять в конце года 105 тысяч рублей при процентной ставке 5 процентов. Либо мы можем выбрать другой способ премирования, когда нам выплачивают по 50 тысяч рублей раз в полгода при той же процентной ставке.
Сравним эти два платежа. Для этого посчитаем, какое будет текущее значение для каждой из данных выплат. Воспользовавшись формулой для нахождения текущего значения, нам нужно продисконтировать 105 тысяч по ставке пять процентов (в данном случае T=1). Получаем 100 тысяч.
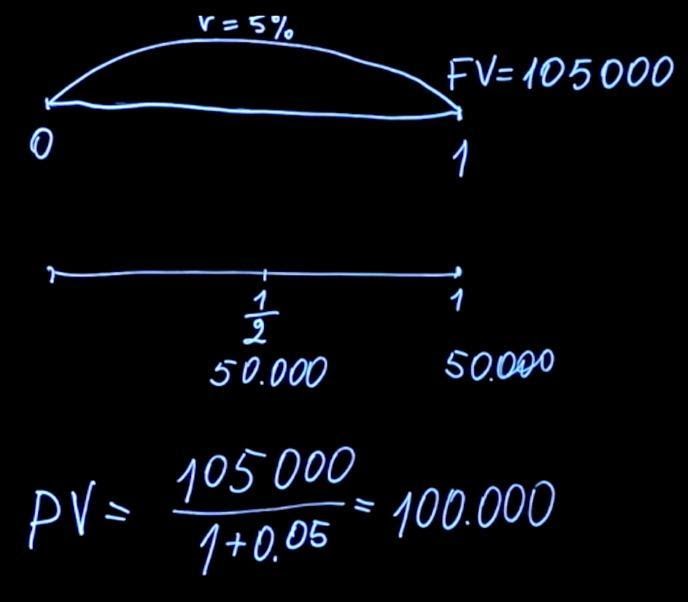
Чтобы найти текущее значение выплат через каждые полгода, мы должны 50 тысяч рублей (которые получим через полгода) продисконтировать по ставке два с половиной процента (потому что начисление происходит только в первые полгода. Строго говоря, ставка на 6 мес не равна половине годовой ставки. N(1+x)(1+x)=N(1+0.05) => x=2.4695% мы инвестируем на 6 мес, а потом опять на 6 и это идентично инвестиции на год), пять процентов годовых, деленные на два, плюс 50 тысяч полученные в конце года, которые мы дисконтируем по ставке 5 процентов. В результате подсчетов мы получаем цену первого платежа за полгода в размере 48780 рублей 49 копеек и второго платежа — 47619 рублей 5 копеек. Сумма ценностей составляет 96399 рублей 54 копеек.
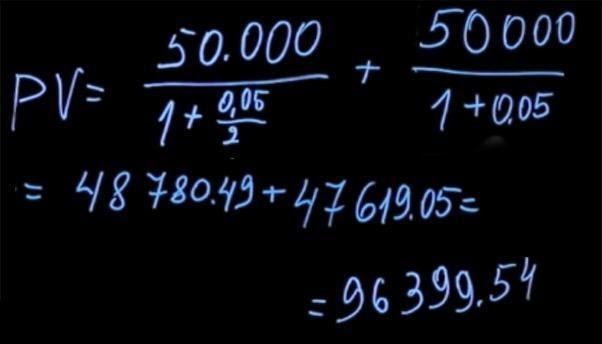
Очевидно, что предложение получить 105 тысяч рублей через год выгоднее, чем получать по 50 тысяч раз в полгода. Хотя интуитивно вам могло показаться, что разница несущественна, при том, что деньги вы получите быстрее. Математика говорит нам о том, что это не так.
Например, когда вам предлагают купить автомобиль в рассрочку или заплатить полную сумму сейчас с какой-нибудь скидкой. Нужно взять будущую сумму, которую вы заплатите, привести к текущему значению, а затем сравнивать платежи, происходящие в один и тот же момент времени.
В таком случае сравнение будет корректным.
#3. Форвардные процентные ставки
Допустим, мы с вами договоримся о процентной ставке. Под эту процентную ставку я через год возьму у вас деньги в долг, которые верну через два года плюс процент. Какова должна быть в данном случае процентная ставка, чтобы она была справедливой? Распишем этот пример подробнее.

Мы находимся сейчас в моменте времени «ноль». Через год я у вас по ставке x возьму деньги и верну их вам через два года. Как рассчитать ставку x ? У нас есть несколько опций. Вы можете сейчас положить деньги по ставке r 1 на год, а затем реинвестировать их по ставке x .

Либо положить деньги сразу по ставке r 2 на два года.
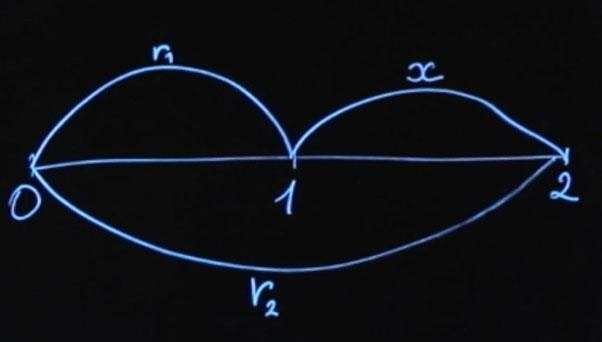
На финансовом рынке существует правило отсутствия арбитража (No-Arbitrage Condition). Оно говорит о том, что если в конце срока мы получаем одинаковые выплаты, то для инструментов с одинаковым риском начальная сумма должна быть тоже одинаковая. Давайте распишем и это. Будущее значение первого варианта инвестиции FV 1 будет равняться текущему значению, умноженному на сумму единицы и rT 1 (будем считать, что у нас простое начисление процентов).
Момент времени T 1 у нас равняется одному году. Дальше у нас произойдет реинвестирование суммы, и мы положим на промежуток времени от T 2— T 1, умноженную на нашу процентную ставку x . T 2 – это момент времени, в нашем случае два года.
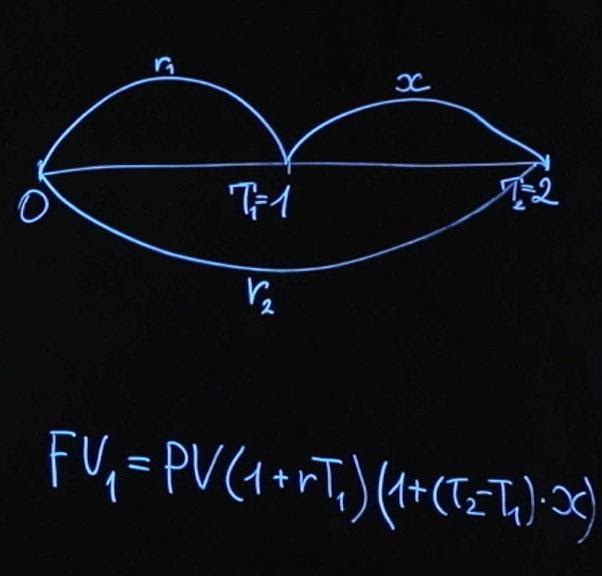
Либо будущее значение FV 2 будет равняться текущему значению PV , умноженному на единица плюс r 2, умноженное на T 2. Согласно условию отсутствия арбитража FV 1 должно равняться FV 2.
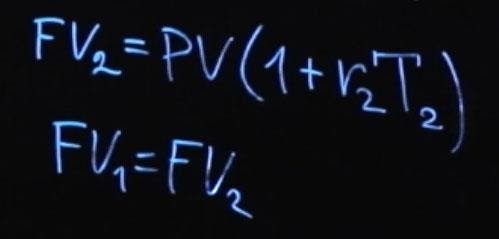
Из этого мы получаем следующее:
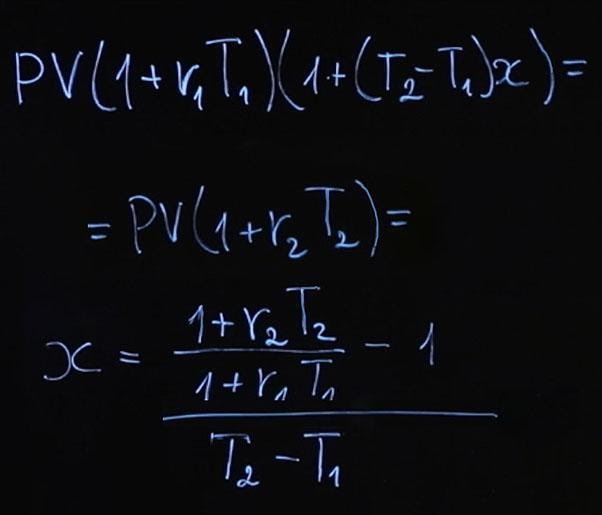
Формула получилась достаточно громоздкая. Давайте рассчитаем по этой формуле пример, а затем подумаем, что мы можем сделать, чтобы она выглядела проще.
Пусть процентные ставки у нас r 1=4%; r 2=6%. В таком случае имеем следующее:
Казалось бы странно, что ставка на два года равняется шести процентам, на год она равняется четырем процентам, а от года до двух мы получаем ставку более семи процентов. Объясняется это так. Поскольку в первый год у нас годовая ставка ниже чем на два года, в следующий год она должна быть выше, чем обе этих ставки. Это необходимо для того, чтобы компенсировать недостаток начисления процентов в первом году, и после реинвестирования можно было бы получить такую же сумму, как при инвестировании на два года по более высокой ставке. Такая ставка называется форвардной процентной ставкой.
Чтобы облегчить себе жизнь, давайте упростим эту формулу. Если мы будем использовать формулу непрерывного начисления процентов ( FV=PVe rT ), то тогда мы можем переписать условие отсутствия арбитража следующим образом:
Если мы возьмем логарифм от обеих сторон нашего равенства и сократим константы, мы получим:
Далее легко найти x:
Согласитесь, такую формулу для будущих процентных ставок использовать гораздо проще и удобнее.
Вы можете задать вопрос – а зачем такой странный продукт и кто им пользуется?
Представьте себе ситуацию, когда у вас или у вашей компании точно будет поступление средств через год. Сейчас вы бы хотели обезопасить себя от риска изменения процентных ставок. Вы понимаете, что через год процентная ставка может увеличиться и стать более выгодной, но также вы понимаете, что она может понизиться. И вам вполне комфортно с действующей на рынке форвардной процентной ставкой. Тогда вы можете заключить контракт, указав в нем, что на те деньги которые поступят в будущем через год, вы заключаете договор по заданной ставке. Ставка фиксируется, и вы больше не переживаете о том, как будут происходить изменения процентных ставок на рынке.
Обратите внимание, что форвардная процентная ставка ни в коем случае не является предсказанием будущей цены. Это абсолютно не значит, что процентные ставки будут равны 7,7% через год, когда мы окажемся в точке T1. Они могут принимать какое угодно значение, и вот почему. В момент, когда мы рассчитываем форвардную процентную ставку из ставок, действующих на рынке, мы можем сказать, что эта ставка является ожиданием рынка относительно будущих цен. Но к моменту, когда мы перемещаемся в будущее, происходят новые события, добавляется новая информация, и рынок каким-то образом меняется. Поэтому процентные ставки через год не будут совпадать с форвардными ставками, рассчитанными на год сейчас.
Источник https://journal.open-broker.ru/economy/chto-takoe-kapitalizaciya-procentov/
Источник https://studref.com/482994/finansy/naraschennaya_summa
Источник https://habr.com/ru/company/dbtc/blog/501566/

